哪懂什么算法，全是靠刷

数学

排列：A(m, n) = n!/(n-m)!
组合：A(m, n) = n!/(m!(n-m)!)

离线查询

在线查询：请求来一个，立即处理并回答一个。

离线查询：把所有请求收集起来，统一处理，统一回答。

离散化思想

在不改变数据相对大小的条件下，对数据进行相应的缩小。

树状数组

最大化最小值、最小化最大值

二分答案

2517. 礼盒的最大甜蜜度

正难则反（逆向思维）

正向求解 = 总数 - 反向求解

贡献思维

求所有方案数 转化为 求每个元素的贡献值的总和

2475. 数组中不等三元组的数目

分解质因数

while i * i <= n:
    while n % i == 0:
        # print(i)
        n //= i
    i += 1

差分数组

多次操作：一个区间内的数都加1
操作完了，需要看一下每个数变成多少了

# 初始数组
[0, 0, 0, 0, 0]

# 区间[1,3]都加上1，把开始的地方+1，在结束的地方-1
[0, 1, 0, 0, -1]

# 区间[0, 1]都加上1，把开始的地方+1，在结束的地方-1
[1, 1, -1, 0, -1]

# 结果，求前缀和
[1, 2, 1, 1, 0]

二分查找

# 返回有序数组中第一个 >= target的位置。如果都小于target，返回数组长度。
def lower_bound(nums: List[int], target: int) -> int:
    # 闭区间 [left, right]
    left = 0
    right = len(nums) - 1

    while left <= right:
        mid = left + (right - left) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return left

# 三种区间
# [left, right]
# [left, right)
# (left, right)
# 上面代码稍微改动即可

def lower_bound2(nums: List[int], target: int) -> int:
    # 左闭右开 [left, right)
    left = 0
    right = len(nums)

    while left < right:
        mid = left + (right - left) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left  # 返回right也可以

def lower_bound3(nums: List[int], target: int) -> int:
    # 开区间 (left, right)
    left = -1
    right = len(nums)

    while left + 1 < right:
        mid = left + (right - left) // 2
        if nums[mid] < target:
            left = mid
        else:
            right = mid
    return right

# 四种情况：
# >= x      获取第一个 >= x的位置
# > x       可以转换成 >= (x+1)
# < x       可以转换成 (>= x) - 1；表示第一个>=x位置的左边位置
# <= x      可以转换成 (> x) - 1；表示第一个>x位置的左边位置；>x还可以继续转换

# 举例：
# 获取有序数组中目标值target的第一个位置和最后一个位置（假设存在target）
start = lower_bound(nums, target)        # >= x
end = lower_bound(nums, target+1) - 1    # <= x

from bisect import *

# bisect_left 查找第一个大于等于target的位置
# bisect 查找第一个大于target的位置
# bisect_right 查找第一个大于target的位置

01背包

dp = [0]*(target+1)
# 求有多少种方法
# dp[0] = 1
for i in range(len(nums)):
    for j in range(target, nums[i]-1, -1):
        # 求最大价值
        dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
        # 求有多少种方法
        # dp[j] += dp[j-nums[i]]
return dp[target]

完全背包

唯一的区别就是背包的遍历顺序：01背包是要求倒序，完全背包是正序

for n in nums:  # 遍历物品
    for j in range(n, target+1):  # 遍历背包
        # 求最大价值
        # 求有多少种方法

先遍历物品

由于先遍历的物品，会得到物品的组合。

比如物品[1,2,3]，背包容量为3。先遍历1，后遍历2，得到组合[1,2]。

for n in nums:  # 遍历物品
    for j in range(c, target+1):  # 遍历背包

先遍历背包

由于先遍历的背包，会得到物品的排列。

比如物品[1,2,3]，背包容量为3。既能得到[1,2]，又能得到[2,1]。

for j in range(0, target+1):  # 遍历背包
    for n in nums:  # 遍历物品

多重背包

dp = [0]*(target+1)
# 求有多少种方法
dp[0] = 1
# 每个物品的价值是value，数量有count个
for count, value in nums:
    for i in range(target, 0, -1):
        for j in range(1, count+1):
            if i - j*value >= 0:
                # 求有多少种方法
                dp[i] += dp[i-j*value]
return dp[target]

6310. 获得分数的方法数

判断一个数是否是2的幂次方

x & (x-1) == 0

取模

取模过程只能乘、加、减，而除法取模只能使用逆元进行操作。

(a + b) % MOD == a % MOD + b % MOD

6368. 找出字符串的可整除数组

前后缀分解

1653. 使字符串平衡的最少删除次数

区间排序

在求多个区间[start, end]的重叠情况时，可以进行按左端点 或 右端点 排序来统计。

这里有一个性质：如果按右端点 排序，前面一个区间和后面一个区间如果存在交集，那么这个交集一定是前面区间的一个后缀。

限定边界的子数组

限定边界的情况下，统计满足条件的子数组，这类问题，可以通过在二维坐标里面画图，来分析思路。

795. 区间子数组个数

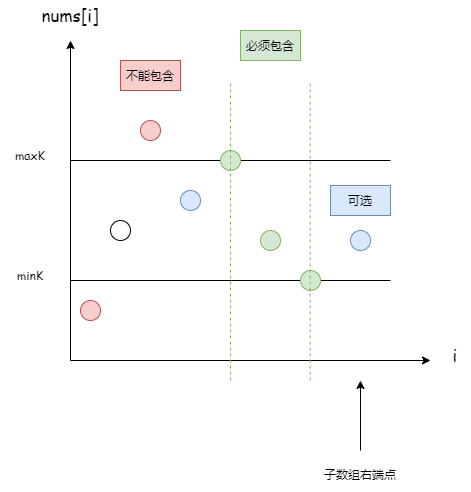
2444. 统计定界子数组的数目

反转链表

## 递归法
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if head is None or head.next is None: return head
        newHead = self.reverseList(head.next)
        head.next.next = head
        head.next = None
        return newHead

## 迭代法
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        pre = None
        cur = head
        while cur:
            nxt = cur.next
            cur.next = pre
            pre = cur
            cur = nxt
        return pre

快排

def partition(self, nums, left, right):
    pivot = left
    j = pivot+1
    for i in range(j, right+1):
        if nums[i] < nums[pivot]:
            nums[i], nums[j] = nums[j], nums[i]
            j += 1
    nums[pivot], nums[j-1] = nums[j-1], nums[pivot]
    return j-1

def quickSort(self, nums, left, right):
    if left < right:
        p = self.partition(nums, left, right)
        self.quickSort(nums, left, p-1)
        self.quickSort(nums, p+1, right)

随机化版本

def randomPartition(self, nums, left, right):
    i = random.randint(left, right)
    nums[i], nums[left] = nums[left], nums[i]
    return self.partition(nums, left, right)

def randomQuickSort(self, nums, left, right):
    if left < right:
        p = self.randomPartition(nums, left, right)
        self.randomQuickSort(nums, left, p-1)
        self.randomQuickSort(nums, p+1, right)

数组中的第K个最大元素

# 快排分区思想：找出一个数的正确位置，使得左边比它小，右边比它大
# 要找出第k大的元素，快排按降序排序，找到第k-1的位置
# partition写成降序

def randomPartitionWithK(self, nums, left, right, k):
    if left >= right:
        return
    # 获取随机位置
    i = random.randint(left, right)
    nums[i], nums[left] = nums[left], nums[i]
    index = partition(nums, left, right)
    # 如果位置大于k，则在左边继续分区
    # 如果位置小于k，则在右边继续分区
    # 如果位置等于k，则停止分区
    if index > k: self.randomPartitionWithK(nums, left, index-1, k)
    elif index < k: self.randomPartitionWithK(nums, index+1, right, k)

def findKthLargest(self, nums: List[int], k: int) -> int:
    self.randomPartitionWithK(nums, 0, len(nums)-1, k)
    return nums[k-1]

技巧篇